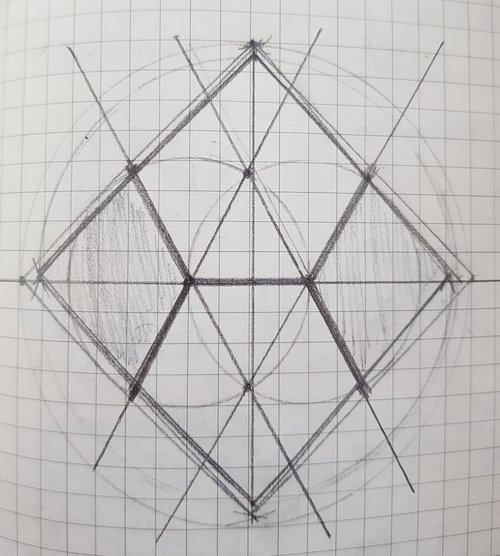
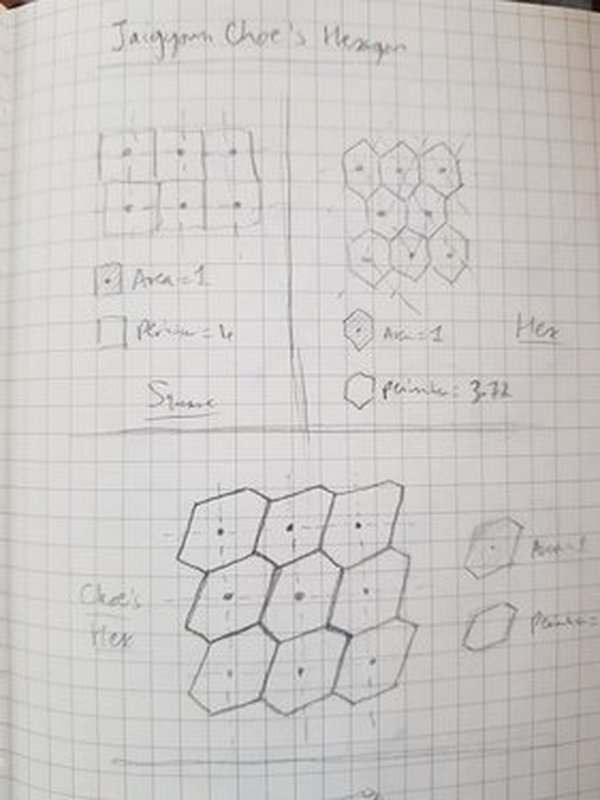
In 1989, Jaigyoung Choe discovered this hexagon (see the paper for details) which is a minimal perimiter shape. Although googling it just now I found this page from Ed Pegg Jr (who I’m pretty sure is on Math.SE) that mentions it was already known from the ‘Cairo pentagonal tiling’ (link) which is dual to a sqare/triangle tesselation.
Anyway, it looks like this:


The second image here is reproduced from this quanta article and shows that this shape has a minimal perimeter when centered on a square grid.
The answer is yes. If you slightly rearrange the parts of the hexagons you get images looking more like this:


Apologies for the second image - the weird button is because I put these A7 items in little plastic wallets and I could not be bothered to take it out…